21.01.2014, Vladimír Klaus, navštíveno 15450x
K napsání tohoto článku mě vedla potřeba zjistit, jak daleko jsou od sebe dvě fotky. Přesněji řečeno, jak hodně špatně se určila poloha u jedné fotky, zatímco u druhé byla zcela korektní, přičemž obě byly pořízené jen pár metrů od sebe.

Na webu se dá najít spousta (šílených) vzorečků, návodů a matematických vysvětlení, jak to celé funguje. Nebojte, takovými detaily se tu zabývat nebudu.
Pro výpočet budeme potřebovat goniometrické funkce. Drobnou komplikací je to, že v Math knihovně očekávají tyto funkce úhel v radiánech. Nejprve si tedy napíšeme jednoduchou převodní funkci.
//pomocná funkce na převod stupňů na radiány
double DegToRad(double uhel) {
return uhel * Math.PI / 180.0;
} Pak už přijde na řadu vlastní výpočet, který vypadá docela sofistikovaně.
//funkce, na výpočet přibližné vzdálenosti dvou míst zadaných
//pomocí dvou zeměpisných šířek a délek
double VzdalenostNaZemi1(double sirka1, double delka1,
double sirka2, double delka2) {
//přibližný "průměrný" poloměr Země (není to koule, takže
//to je na různých místech různé)
var R = 6371;
//zjistím rozdíl šířek a délek
var rozdilSirek = DegToRad(sirka2-sirka1);
var rozdilDelek = DegToRad(delka2-delka1);
sirka1 = DegToRad(sirka1);
sirka2 = DegToRad(sirka2);
var a = Math.Sin(rozdilSirek/2) * Math.Sin(rozdilSirek/2) +
Math.Sin(rozdilDelek/2) * Math.Sin(rozdilDelek/2) *
Math.Cos(sirka1) * Math.Cos(sirka2);
var c = 2 * Math.Atan2(Math.Sqrt(a), Math.Sqrt(1-a));
var d = R * c;
//vrátím vzdálenost v kilometrech
return d;
} Je tu ale ještě jedna jednodušší funkce, jak určit vzdálenost na povrchu koule.
//jednodušší, přesto přesná (srovnatelná) metoda
double VzdalenostNaZemi2(double sirka1, double delka1,
double sirka2, double delka2) {
sirka1 = DegToRad(sirka1);
delka1 = DegToRad(delka1);
sirka2 = DegToRad(sirka2);
delka2 = DegToRad(delka2);
return 6371 * Math.Acos(
Math.Sin(sirka1) * Math.Sin(sirka2)
+ Math.Cos(sirka1) * Math.Cos(sirka2)
* Math.Cos(delka2 - delka1));
} Jako příklad můžeme vzít tyto souřadnice.
GPS 1 = 50.128328, 14.493012
GPS 2 = 50.126062, 14.443097
Výsledek obou funkcí je v podstatě identický.
vzdálenost 1 = 3,56712317650752
vzdálenost 2 = 3,56712317775145
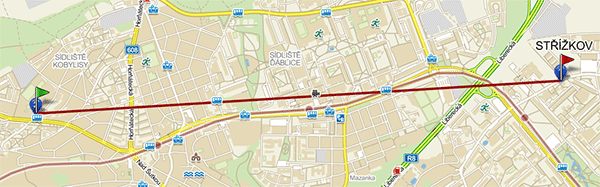
Obě funkce VzdalenostNaZemi() nám tedy vracejí 3,567 km, zatímco měření na mapy.cz ukáže 3,577 km. Rozdíl je tedy pouhých 10 m, což je myslím vynikající. Nemám ponětí o tom, jak Seznam určuje vzdálenosti a tak nelze říci, co je přesnější. Pro mě bylo a je důležité, že funkce splnila účel a její naprogramování nebylo náročné.
Pokud budete zadávat polohu ze západní/jižní polokoule, nezapomeňte, že hodnoty musí být záporné. Například New York je na severní polokouli (+40 st. severní šířky), ale zároveň je také na západní polokouli (-74 st. západní délky). Zde jsou údaje pro Sochu Svobody a Central Park.
GPS 1 = 40.68962, -74.045647
GPS 2 = 40.782361, -73.965996
Vzdálenost opět vychází stejně, při měření na Google mapách je výsledek 12,3175 km, tedy opět rozdíl jen asi 14 m.
vzdálenost 1 = 12,3037262216122
vzdálenost 2 = 12,3037262213739
Pro nadšené matematiky uvádím ještě odkaz na další povídání a pěkné vzorečky.
